Page 23 - MECÁNICA PARA INGENIERÍA Y SUS APLICACIONES – DINÁMICA Capítulo II

MECÁNICA PARA INGENIERÍA Y SUS APLICACIONES – DINÁMICA Capítulo IV


W 1 2  t 2 M  k dt   2  M d [4.5.1.4.8.1]

Z
t 1 1 
Si, el momento en Z es constante, el trabajo del par es:

W 1 2  M Z  2  1  [4.5.1.4.8.2]


Nota 1.- Si el trabajo es positivo, nos indica que cuerpo gira en la dirección del momento.

Nota 2.- Para fuerzas conservativas, es válido todo lo deducido para un sistema de partículas.

Ejemplos:

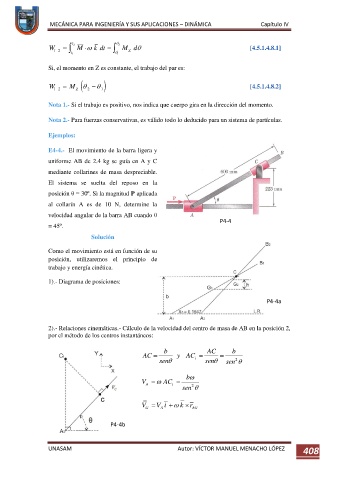
E4-4.- El movimiento de la barra ligera y
uniforme AB de 2.4 kg se guía en A y C

mediante collarines de masa despreciable.
El sistema se suelta del reposo en la

posición θ = 30º. Si la magnitud P aplicada
al collarín A es de 10 N, determine la
velocidad angular de la barra AB cuando θ
P4-4
= 45º.
Solución

Como el movimiento está en función de su
posición, utilizaremos el principio de
trabajo y energía cinética.

1).- Diagrama de posiciones:

P4-4a

2).- Relaciones cinemáticas.- Cálculo de la velocidad del centro de masa de AB en la posición 2,
por el método de los centros instantáneos:

b AC b
AC  y AC  
2
sen  i sen  sen 

b
V   AC 
i
A
sen 
2

V  V i   k r
AG
G
A
P4-4b

UNASAM Autor: VÍCTOR MANUEL MENACHO LÓPEZ 408